Generative Adversarial Networks
Generative Models Review
Autoregressive Models directly maximize likelihood of training data \(p_{\theta}(x)=\prod_{i=1}^N p_{\theta}(x_i|x_1,\dots,x_{i-1})\)
Variantional Autoencoders introduce latent feature $z$, and maximize the lower bound \(p_{\theta}(x)\ge E_{z\sim q_{\phi}(Z|X)}[\log p_{\theta}(x|z)]-D_{KL}(q_{\phi}(z|x),p(z))\)
Generative Adversarial Networks give up on modeling $p(x)$, but allow us to sample from $p(x)$
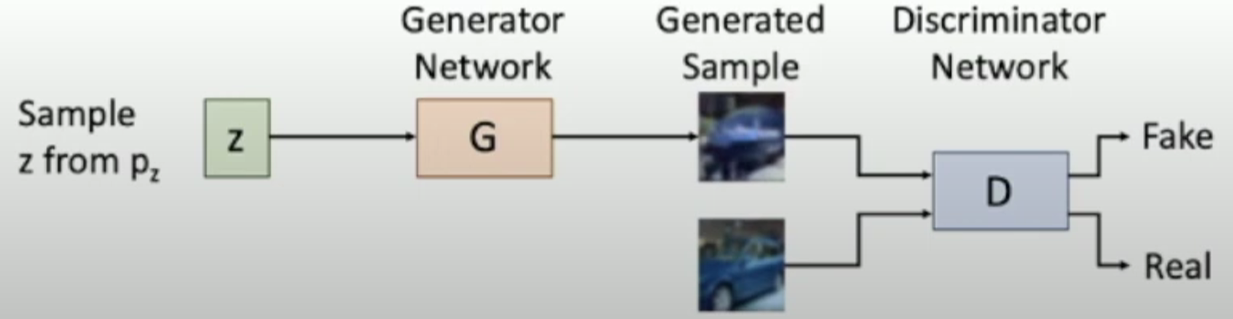
Intuition of GAN
Assume we have data $x$ drawn from distribution $p_{data}(x)$ and we want to sample from $p_{data}$.
First we introduce a latent variable $z$ with simple prior $p(z)$.
Sample $z\sim p(z)$ and pass to a Generator Network $x=G(z)$.
Then $x$ is a sample from the Generator distribution $p_G$ and we want $p_G=p_{data}$.
Train Generator Network G to convert $z$ into fake data $x$ sampled from $p_G$ by “fooling” the discriminator D.
Train discriminator D to classify the data as real or fake.
Jointly train G and D $\rightarrow$ make $p_G$ converge to $p_{data}$.
Training Objective of GAN
Jointly train G and D with a minimax game \(\min_G \max_D (E_{x\sim p_{data}}[\log D(x)]+E_{z\sim p(z)}[\log(1-D(G(z)))])\\ =\min_G \max_D V(G,D)\)
The 1st term: Discriminator wants $D(x)=1$ for real data.
The 2nd term: Discriminator wants $D(x)=0$ for fake data while Generator wants $D(x)=1$ for fake data(i.e., G is trying to compete with D by imitating $p_{data}$).
Use alternating gradient updates to train G and D:
For timestep $t$:
Update $D$ \(D=D+\alpha_D\frac{\partial V}{\partial D}\\\)
Update $G$ \(G = G - \alpha_G \frac{\partial V}{\partial G}\)
Problem: At start, Generator is very bad and D can easily tell apart real/fake, so $D(G(z))$ is close to 0, causing vanishing gradients for G.
Solution: Instead of training minimize $\log (1-D(G(z)))$, train G to maximize $-\log(D(G(z)))$. Then G gets strong gradients at start of training.