UMich DL for CV

Recurrent Neural Networks

Key idea

RNNs have an “internal state” that is updated as a sequence is processed, the recurrence formula looks like $h_t = f_W(h_{t-1},x_t)$.

Here $h_t$ is the state at time step $t$, $x_t$ is the input at time step $t$ and $f_w$ is a function with parameters $W$.

Vanilla RNNs

The state consists of a single hidden vector $h$

$h_t = tanh(W_{hh}h_{t-1}+W_{xh}x_t)$

$y_t = W_{hy}h_t$

Backpropagation Through Time

Forward through entire sequence to compute loss

Backward through entire sequence to compute gradient

But : Very long sequence takes a lot of memory $\rightarrow$ Use chunks of the sequence instead of the entire sequence(Truncated Backpropagation Through Time), use the final hidden state of the previous chunk as the first hidden state in the next chunk ($\large h_{t,i}=h_{0,i+1}$)

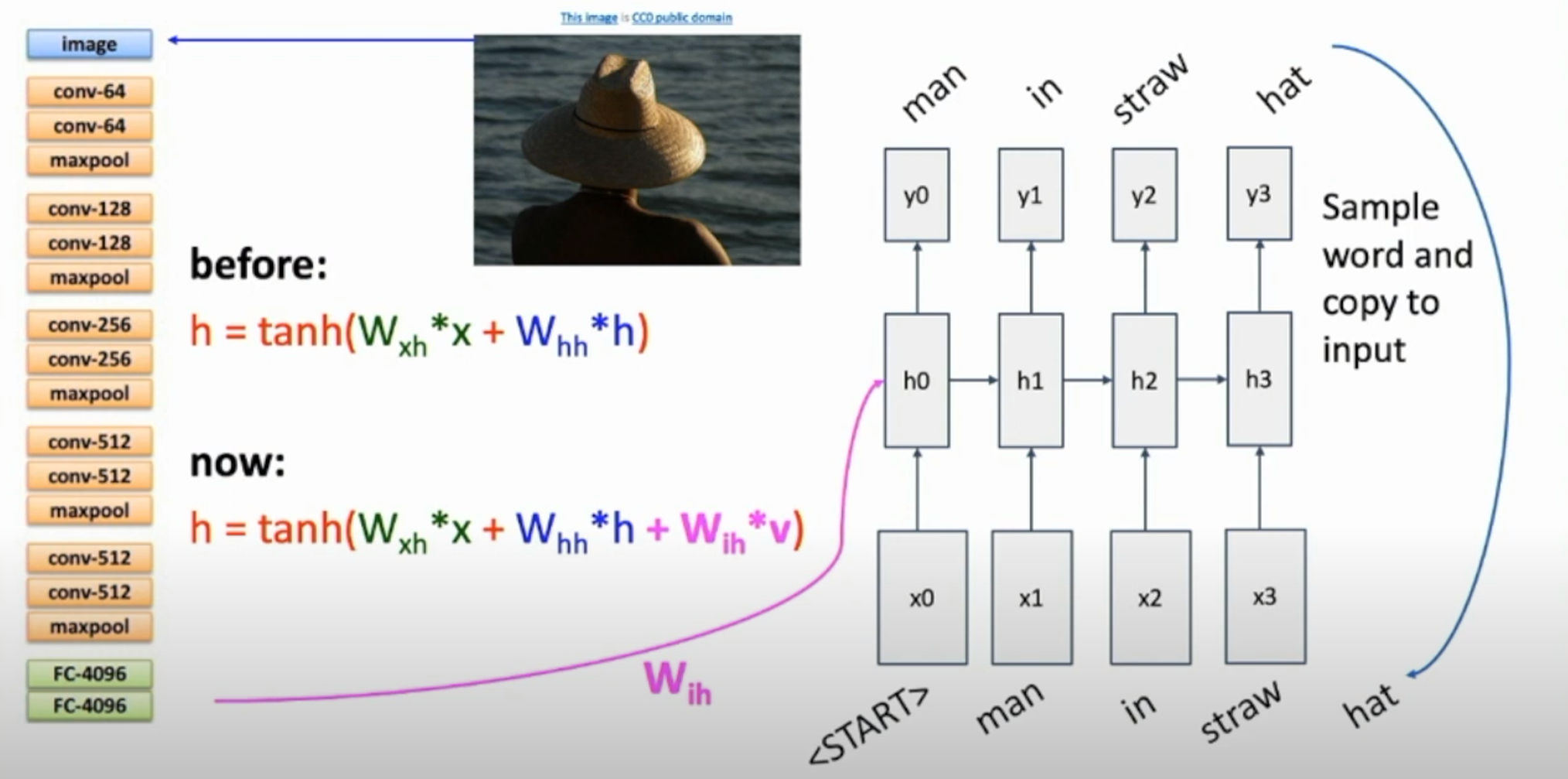
Image Captioning

Image $\rightarrow$ CNN $\rightarrow$ RNN

Transfer learning : Take CNN trained on ImageNet and chop off the last FC layer. In RNN, we’ll have \(h_t = tanh(W_{xh}\times x+W_{hh}\times h_{t-1}) + W_{ih}\times v\) Here $ v $ represents the feature extracted by the CNN.

Vanilla RNN Gradirnt Flow

After stacking this gradient flow, here comes a big problem : compute gradient of $h_0$ involves many factors of W and repeated tanh. If the largest singular value in W > 1, then there will be exploding gradients; if <1, then vanishing gradients.

For exploding gradients we can just scale the gradients when it > threshold, which gives a wrong gradients but at least it won’t cause expoding.

For vanishing gradients, we need to change RNN architecture, and thus Long Short Term Memory(LSTM) was invented.

LSTM

LSTM uses two states, the hidden state $h$ and the cell state $c$

$i$ : Input gate, whether to write cell

$f$ : Forget gate, whether to erase cell

$o$ : Output gate, how much to reveal cell

$g$ : Gate gate, how much to write to cell

\(\begin{bmatrix}i\\f\\o\\g\end{bmatrix}= \begin{bmatrix}\sigma \\ \sigma \\ \sigma \\ tanh\end{bmatrix}W\begin{bmatrix}h_{t-1}\\x_t\end{bmatrix}\) , Here $\sigma$ is the sigmoid function $\large\sigma(x) = \frac{1}{1+e^{-x}}$

$c_t = f \odot c_{t-1} + i \odot g$

$h_t = o \odot tanh(c_t)$

so $i,f ,o \in (0,1)$ $g\in (-1,1)$. Here $\odot$ means elementwise multiplication.

• Previous
  UMich DL for CV
• Next
  UMich DL for CV