UMich DL for CV

Convolutional Network

Why Convolutional Network?

So far our classifiers don’t respect the spatial structure of images (merely stretch pixels into column).

Thus new operators is needed to handle the 2D images, including Convolution Layers, Pooling Layers and Normlization Layers.

Convolutional Layers

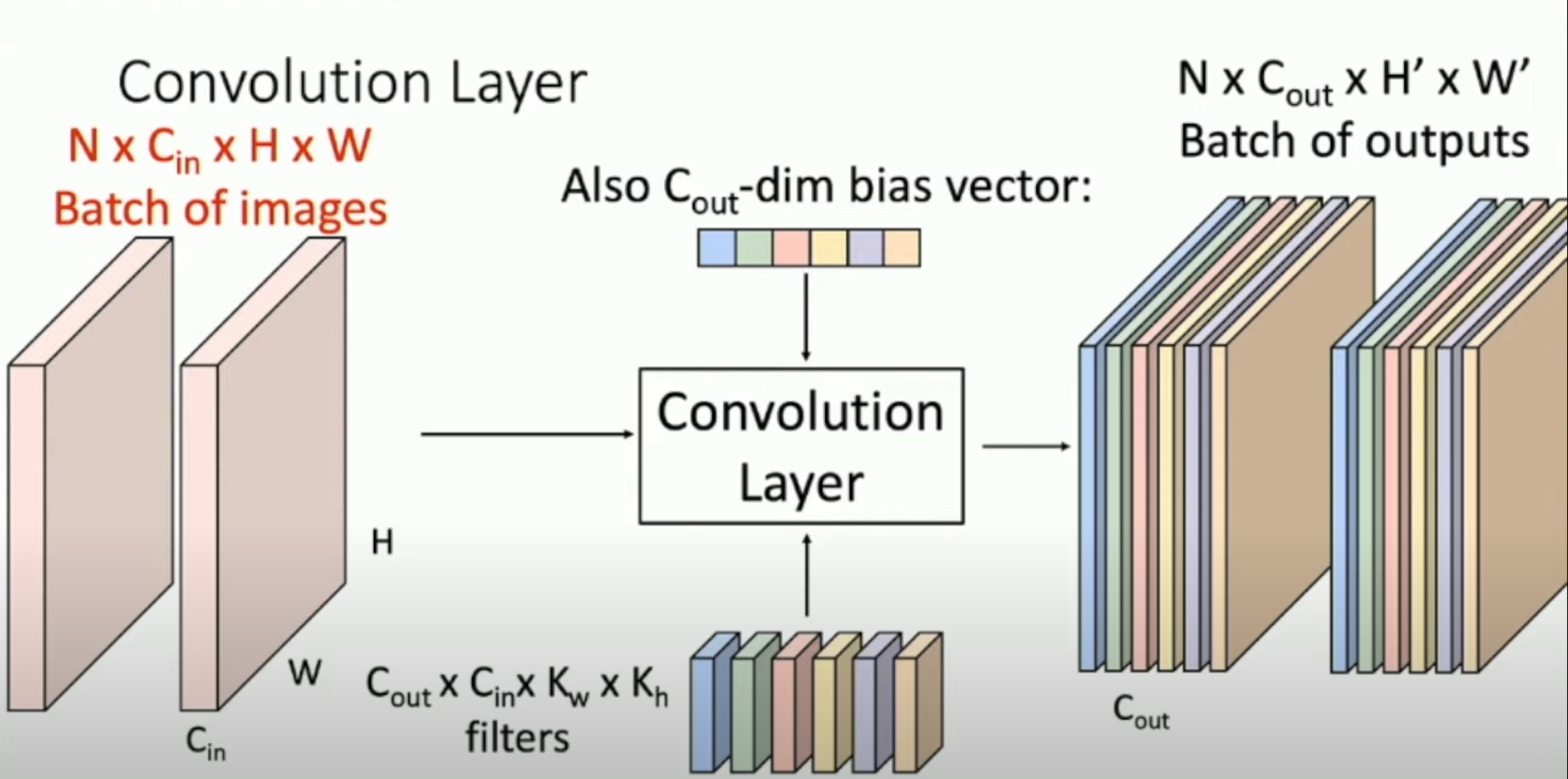
In Fully-Connected Layer, we simply stretch a 32x32x3 image to 3072x1

In Convolutional Layer, we use a filter, with a smaller height & weight but the same depth (e.g., 5x5x3) to slide over the image spatially and compute dot products.

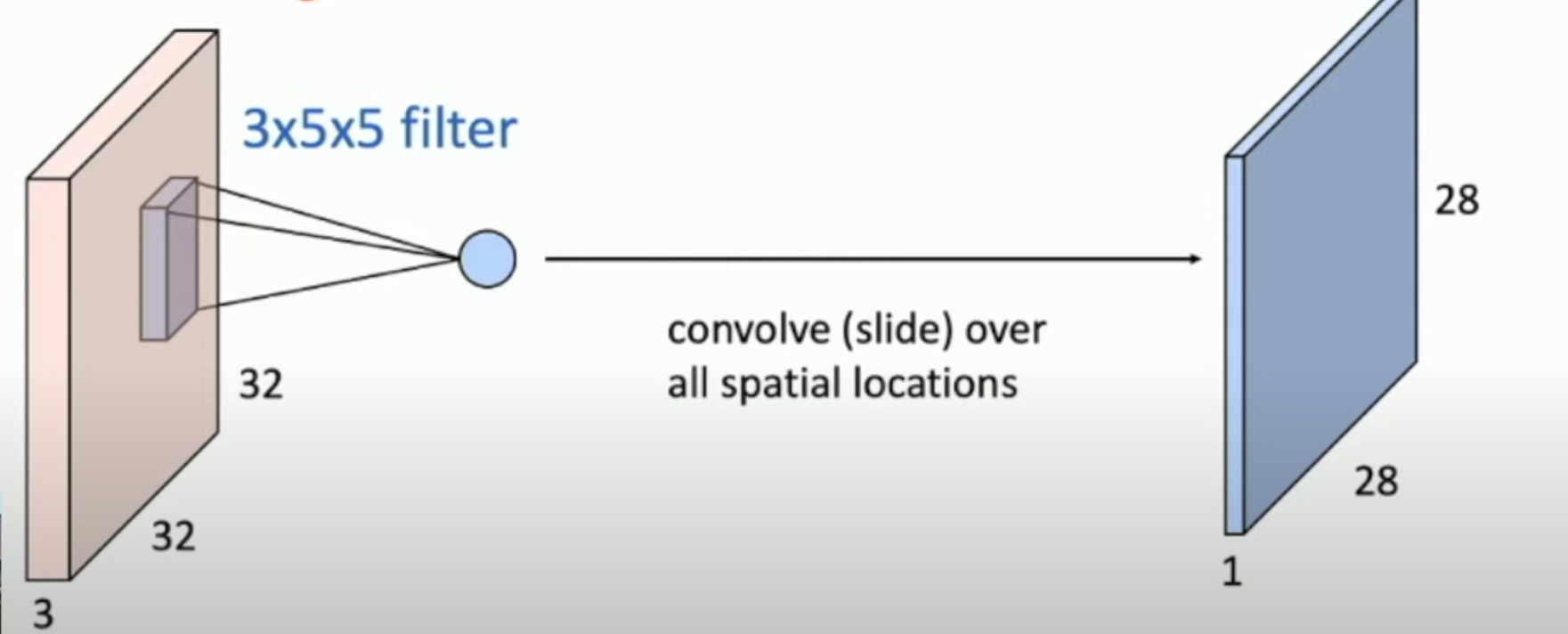
And this convolving procedure can be repeated with different filters to generate more activation maps. This operation can also be performed in batches, as shown in the figure below.

Lec7-Layer Batches.png

padding

Here we notice that convolution operation will shrink the size of the image $H’ = H - K_h+1$, $W’=W-K_w+1$ Thus Padding is introduced to fix this problem by adding extra 0 around the image.

Receptive Field(感受野)

For convolution with kernel size K, each element in the output depends on a K$\times$K receptive field in the input.

So here is another problem: for large images we need many layers for each output to “see” the whole image.

The solution is simple : Downsample inside the network.

Strided Convolution

In each step, the kernels move more than 1 pixels. Generally, if the Input size is W * W, the Filter is

K*K, the padding size is P and the stride is S, then the output size will be : $\frac{W-K+2P}{S}+1$

Pooling Layer

The Pooling Layer is another way to downsample instead of using stride in Convolution Layer.

The Hyperparameters include Kernel Size, Stride and Pooling Function.

Max Pooling

Max Pooling with 2*2 kernel size and stride 2 looks like ：

1  1  | 2  4 
5 (6) | 7 (8) 					6	8
-------------			-->		
(3) 2 | 1  0					3	4
 1  2 | 3 (4) 

Since the kernel size is equal to the stride, this is a non-overlapped pooling.

Batch Normalization

The idea of Batch Normalization is normalizing the outputs of a layer so they have zero mean and unit variance, which helps reduce “internal covariate shift” and improves optimization.

What is internal covariate shift?

Internal covariate shift refers to the phenomenon where the distribution of inputs to each layer of a neural network changes during training as the parameters of previous layers are updated. This happens because, as the model weights are adjusted, the inputs to subsequent layers also change, which can slow down training and make convergence harder.

In Convolutional Neural Networks (CNNs), this shift can be especially noticeable because the network typically has many layers, and as each layer updates, the distributions of activations can change drastically. The network has to continuously adapt to these new distributions, which can lead to instability and inefficient learning.

Normalize

for input $x : N\times D$, $N$ is the channel size, $D$ is the batch size.

$\mu_j$ is the per-channel mean, shape is $(D,)$

$\sigma_j$ is the per-channel std, shape is $(D,)$

$\hat{x}_{i,j}$ is the normalized input, shape is $N\times D$

\[\mu_j = \frac{1}{N}\sum_{i=1}^{N}x_{i,j} \\ \sigma^2_j = \frac{1}{N}\sum_{i=1}^{N}(x_{i,j}-\mu_j)^2 \\ \hat{x}_{i,j} = \frac{x_{i,j} - \mu_j}{\sqrt{\sigma_j^2+\epsilon}}\\\]

However, there is a problem : zero-mean, unit variance — too hard as a constraint.

So in pratice we use learnable scale and shift parameter $\gamma,\beta$ with shape $(D,)$ for output $y_{i,j} = y_j\hat{x}_{i,j}+\beta_j$.

There is another problem: during testing, the data in a batch may not be accessible simultaneously!

So in test-time, $\mu_j$ and $\sigma_j^2$ will be the average of values seen during training.

In this situation, the batchnorm becomes a linear operator(since the two parameters are constants now). Thus in pratice batchnorm can be fuse with the previous fully-connected or convolution layer!

CNN Architecture

AlexNet(2012) and ZFNet(2013) have 8 layers but no certain rule, just trial and error.

VGG(2014) is the first CNN to have regular design and deeper network. In VGG, all conv are 3*3 with stride 1 padding 1, all maxpool are 2*2 with stride 2. After pool, double #channel.

VGG16 has 5 convolutional stages :

Stage1 : Conv-Conv-Pool

Stage2 : Conv-Conv-Pool

Stage3 : Conv-Conv-Pool

Stage4 : Conv-Conv-Conv-Pool

Stage5 : Conv-Conv-Conv-Pool

For VGG19, there are 4 Conv in Stage4 and Stage5.

Why 3*3 Conv Kernels?

In terms of receptive field, a single 5*5 Conv (output = $x-5+1$) is the same with double 3*3 Conv (output = $(x-3+1)-3+1$). However, the params and FLOPs are $25C^2$ and $25C^2HW$ for the 5*5 Conv while $18C^2$ and $18C^2HW$ for the 3*3 Conv.

Therefore, using two 3*3 can reduce parameters and take less computation. What’s more, there is an extra ReLu between two Conv which provides more depths and non-linear computation!

Why 2*2 maxpool?

All Conv layers preserves the same FLOPS.

GoogLeNet(2014) focus on efficiency.

Stem network at the start aggressively downsamples input (since most of the compute was at the start)
Inception module: local unit with parallel branches, use 1*1 bottleneck conv layer to reduce channel dimension before expensive conv.
Global average pooling : instead of big fully-connected layers, GAP takes the average of all the values in the feature maps (output of the last conv layer) across all spatial dimensions (height and width), but not across the depth (channels)

ResNet(2015)

When the network goes deeper, the training process can become more difficult due to issues like vanishing gradients which hurts the performance. Deep networks fail to propagate gradients back through many layers.

Thus, ResNet proposed the Residual Block.

Instead of learning the direct mapping from input $x$ to output $H(x)$, the network learns the residual mapping $F(x)$, which we have $H(x) = F(x) +x$.

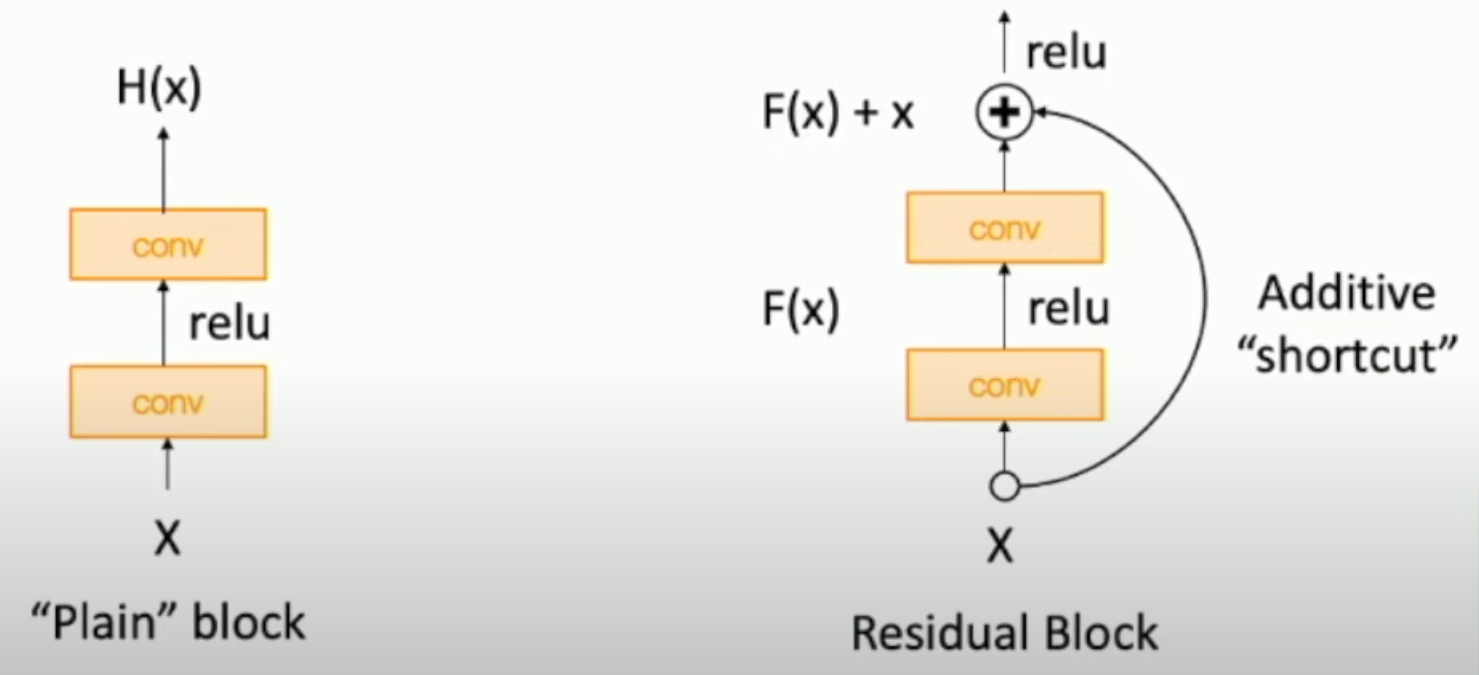
Note that ReLU after residual cannot actually learn identity function since the outputs are non-netgative. But ReLU inside residual can learn true identity function by setting conv weights to 0.

(1) Original ResNet Block
o --> Conv - BatchNorm - ReLu - Conv - BatchNorm @ - ReLu
|												 ^
v------------------------------------------------|


(2) "Pre-Activation" ResNet Block
o --> BatchNorm - ReLU - Conv - BatchNorm - ReLU - Conv @ 
|														^
v-------------------------------------------------------|

Convoluntional Network