Papers PPoPP Sparse Matrix

PPoPP'24 RoDe Approach

A Row Decomposition-based Approach for SparseMatrix Multiplication on GPUs

Posted by Sirin on October 31, 2024

RoDe-based approach for SpMM and SDDMM

概述

本文是针对SpMM和SDDMM两个kernels给出了一种基于行分解的方法，采用的是Compressed Sparse Row格式来存储稀疏矩阵。通过将稀疏矩阵的行分解为Regular part和Residual part来分别进行计算优化，并设计了相应的负载均衡和细粒度Pipelining技术。

相关技术介绍

CSR格式

CSR格式是一种被广泛用于表示稀疏矩阵的方法。

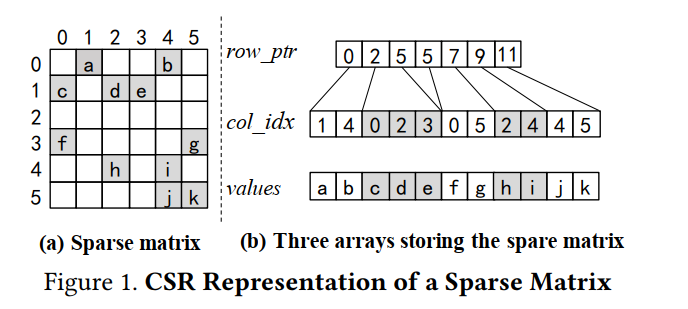
CSR.png

对于CSR格式，其一共使用三个数组来表示系数矩阵的信息，以图中信息为例

  • values数组，从左到右从上到下，记录稀疏矩阵中的非零元素值。 该数组大小等于非零元素的数量
  • col_idx数组，记录每个非零元素值的列信息。 该数组大小等于非零元素的数量。
  • row_ptr数组，row_ptr[i]记录了矩阵第i行元素的在col_idx中的开始位置，row_ptr[i+1]记录了矩阵第i行元素在col_idx中的结束位置。 例如，对于矩阵第0行，row_ptr[0]=0 , row_ptr[1]=2，即说明第一行共有2-0=0个元素，占据了col_idx[0] col_idx[1]对应的两列。 对于矩阵第1行，row_ptr[1]=2,row_ptr[2]=5，说明第二行共有5-2=3个元素，占据了col_idx[2],col_idx[3],col_idx[4]对应的三列。 该数组大小为行数+1，图中矩阵有6行，因此row_ptr数组大小为7。

SpMM

Sparse Matrix-Matrix Multiplication 稀疏矩阵乘以稠密矩阵

核心思想是利用稀疏矩阵的稀疏性来减少计算量。在实际操作中，只有非零元素参与乘法运算，这大大减少了与稠密矩阵相乘时的浮点运算次数。稀疏矩阵通常以压缩存储格式（如CSR、CSC等）保存，以进一步减少内存占用和提高访问效率。

//Input : CSR A[M][N], dense B[N][K]
//Output : dense C[M][K]
for(int i = 0; i < M; i++)//row index从0到M-1，row_ptr[M]是通过i+1(i=M-1时)来访问的
{
	for(int j = A.row_ptr[i]; j < A.row_ptr[i+1]; j++)
	{
		for(int k = 0; k < K; k++)
		{
			C[i][k] += A.values[j] * B[ A.col_idx[j] ][k]
		}
	}
}

SDDMM

Sampled Dense-Dense Matrix Multiplication 采样稠密-稠密矩阵乘法

SpMM和SDDMM在图神经网络中都有应用，因为GNN中邻接矩阵往往是稀疏的，而特征矩阵是稠密的。同样的稀疏矩阵在科学计算中也有应用，例如LOBPCG和iterative solvers with multiple right-hand sides。

//Input : CSR A[M][N], dense B1[M][K] B2[N][K]
//Output : CSR C[M][N]
for(int i = 0; i < M; i++)
{
	for(int j = A.row_ptr[i]; j < A.row_ptr[i+1]; j++)
	{
		for(int k = 0; k < K; k++)
		{
			C.values[j] += B1[i][k] * B2[ A.col_idx[j] ][k]
		}
		C.values[j] *= A.values[j];
	}
}

对于SpMM和SDDMM在GPU上实现并行时，通常先对最外层的i循环进行并行，每个warp/thread block处理一行，warp/thread block内则针对最内层的k循环进行并行。

相关工作

  • 利用优化后的SpMV，将稠密矩阵分解为稠密向量，或者是直接使用SpMV的优化策略来优化SpMM并不能取得很好的效果(因为数据重用模式的差异)

  • ASpT方法提出了自适应的分块技术来提高稀疏矩阵的数据局部性，通过列重排来构建dense tile
  • Sputnik提出了ROMA方法来对sparse rows进行正则化从而使其可以应用vector memory指令，并提出了row swizzle技术在GPU上实现负载均衡
  • 这些工作存在的问题：缺少稠密列(Scarcity of dense columns)会导致ASpT表现不佳甚至出现Slowdown的情况；长短行的不均匀分布(uneven distribution of long and short rows)会导致Spuntnik提出的技术受限。
  • SpMM只对那些不规律分布的非0元素进行内存访问和计算，这导致了稀疏矩阵和稠密矩阵之间存在数据依赖问题，访问稠密矩阵的高延迟访存难以掩盖。

非0元素分布的研究

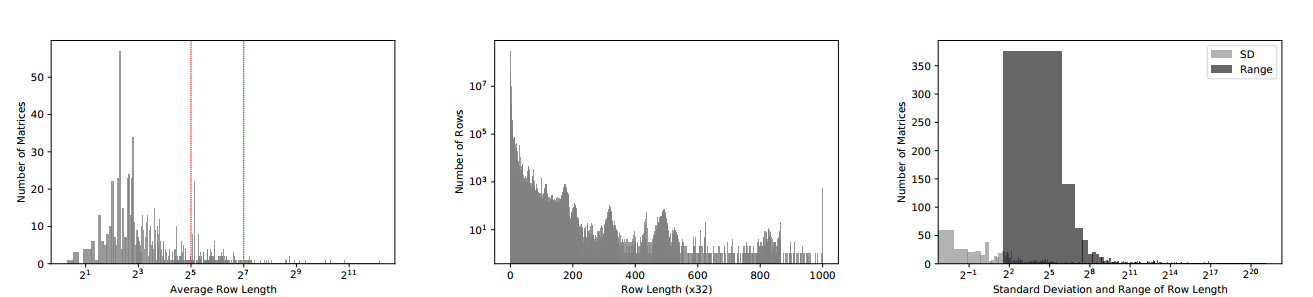
NonzerosDistribution.png

在SuiteSparse上进行统计

  1. 第一张图中可以发现，大部分行的长度是小于32的(32是一个warp内的线程数)，因此为每一行分配一个warp实际上浪费了资源。
  2. 第二张图中表明，虽然绝大多数的行长度小于32，但仍有一部分行的长度达到了1000。
  3. 第三张图中，对于绝大多数矩阵，标准差(Standard Deviation)较小，说明大部分矩阵行的平均长度十分接近；而极差(Range)则偏大，说明有极少部分的行的长度远远偏离了平均长度。这表明大部分稀疏矩阵都是由大量的短行和少数的长行组成的。

特征1中，大量的短行成为了充分利用GPU的计算和访存资源的瓶颈。

特征2表明针对长行进行优化也能够带来一定的收益。

特征3则表明1与2反应的情况在大部分稀疏矩阵中同时存在。

SpMM流水线

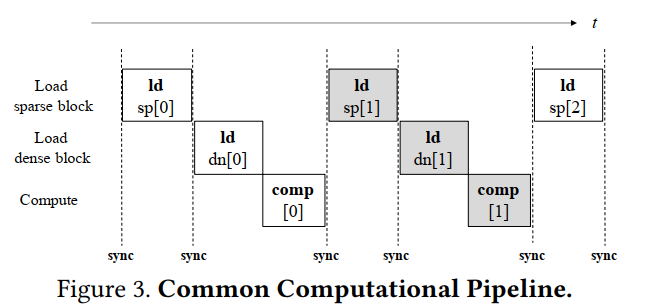
CommonPipeline.png

Sync存在的原因：To enable the reuse of sparse blocks among threads

RoDe

Overview.png

RoDe方法首先将稀疏矩阵的每一行分为block part和residual part，之后通过block split方法对block part进行划分以实现负载均衡，最后通过构建sub-block pipeline在连续的同步操作之间实现更多操作以更好地掩盖访存开销。

Row Decomposition

行分解首先是将每一行分解为若干个block part，每个block part含有32的整数倍个非0元素(32即一个warp内的线程数)。如下图的例子所示，所有满足这一大小的块被放入到(a)代表的block part中，少于32元素的则被放入residual part中。并用两个数组来记录相关信息，Row Indices[]负责记录当前这一块是属于哪一行的；Start Offsets记录了该part的首个元素在原本的若干行中的位置，例如对于residual part #2，其原本的位置应该是#0长度+#1长度+#2的block_part长度，即$24+32+32\times 3=152$ 。

相应的计算可以如下表示

For (a)\\
Start_Offsets_(a)[i]=row_ptr[Row_Indices_(a)[i]]
For (b)\\
Let r_idx=Row_Indices_(b)[i] N_B=32\\
Start_Offsets_(b)[i]=row_ptr[r_idx+1]-(row_ptr[r_idx+1]-row_ptr[r_idx])%N_{B}

第二个算式比较复杂，这里结合例子来说明，比如对于#2的(b)部分来说，后半部分括号内的算式实际上就是row_ptr[3]-row_ptr[2]，那么结合CSR中row_ptr的含义，这个式子实际上算的就是原本#2整行里面的非0元素数，即104，104%32=8，实际上就是#2的residual part的元素数，而前半部分row_ptr[3]实际上反映了前三行(即#0 #1 #2)总的非0元素数，即23+32+104=160，前三行总的元素数减去#2的residual part里面的元素数，自然就是#2 residual中首个元素在原本所有元素中的offset了，即160-8=152。

RoDeExample.png

Block Split

非零元素分布的特征2和特征3表明，同一个矩阵的不同行长度可能会存在较大的差异，因此，需要保证负载均衡。因此，对于row decomposition后的Block part还需要进一步的划分。

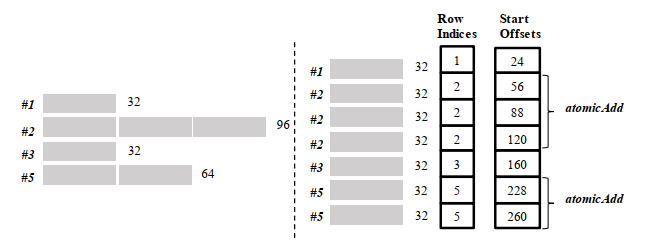
blocksplit.png

这里每个block part又按照Ns的固定大小被划分为若干块，每块都有对应的Row Indices来说明它们原本属于哪一行，Start Offsets则用于说明这一块的首个元素的Index，例如对于#2的第二块，其offset就是#0长度+#1长度+#2的第一块长度，即24+32+32=88。

之后这些块都被当作单独的一行进行处理，原本属于同一行的块通过atomicAdd指令获取结果。尽管atomicAdd会引发额外的开销，通过调整Ns的大小，可以实现比较好的负载均衡折中(实际应用中将Ns设定为512)。

该部分相关计算如下所示

thread index=t_idx
N_B=32 N_S=512
rowLen = row_ptr[t_idx+1]-row_ptr[t_idx]
n_{res}=rowLen % N_B >0  //res部分数量
n_{blk} = floor(rowLen / N_S)+(rowLen > N_B) //block部分数量
N_{res} = prefixSum(n_{res}) //res部分数组标记序数
N_{blk} = prefixSum(n_{blk}) //block部分数组标记序数
if n_{res} > 0 
	Row_Indices_{res}[N_{res}]=t_idx
for i=0 to N_{blk}:
	Row_Indices_{blk}[N_{blk}+i]=t_idx
	Start_Offsets_{blk}[N_{blk}+i]=row_ptr[t_idx]+i * N_S
Sub-block Pipeline

在前图所示的传统的load-computation pipeline中，访问global memory会带来较大的开销。Sub-block pipeline方法的作用就在于更好的重叠shared memory访问、global memory访问和计算。该方法的principle很简单，就是在高延迟的访存进行时，尽可能的issue更多的指令或者进行更多计算。

subblockpipeline.png

为了提升数据重用性，Sparse blocks被加载进shared memory中，而dense blocks的列向量则直接加载到每个线程的寄存器中，累计计算结果也是存储在寄存器中。因为load sparse block的时候需要使用col_idx来获取相应的dense block中的行，因此在load dense block之前必须进行一次同步，保证所有线程都获取到了col_idx的值。

由于sparse block与dense block之间的数据量存在较大差异，因此，在加载完sparse block[0-1]之后，可以先加载dense block[0]，然后在进行[0]上的计算时，加载dense block[1]，在计算[1]的时候，完成sparse block[2-3]的加载，依次类推，实现流水线的重叠，掩盖访存延迟。

SpMM Kernel实现

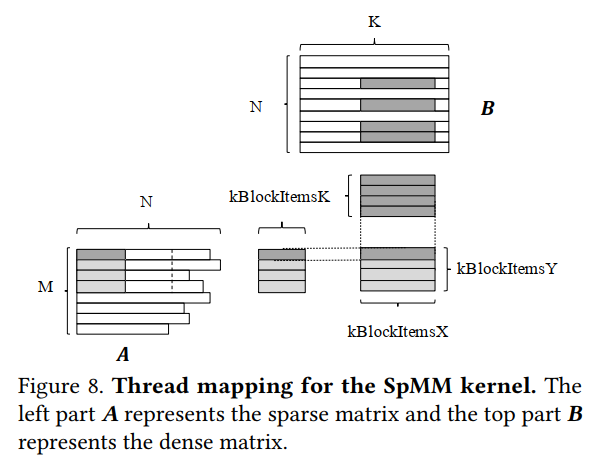
SpMMKernel.png

上图中的两种深色部分表示每个thread block每次计算的部分。颜色更深的那种代表了一次sparse block part与dense block part的相乘计算，即sparse的一行的一部分去依次乘以dense的好几个列，得到相应的结果。

Block part的计算实现

SpMMblock.png

1-3行：计算分块索引并进行thread mapping

4-7行：进行row decomposition和block split操作

10-27行：进行sub-block pipeline

29行：通过atomicAdd操作进行累加

Residual part的计算实现

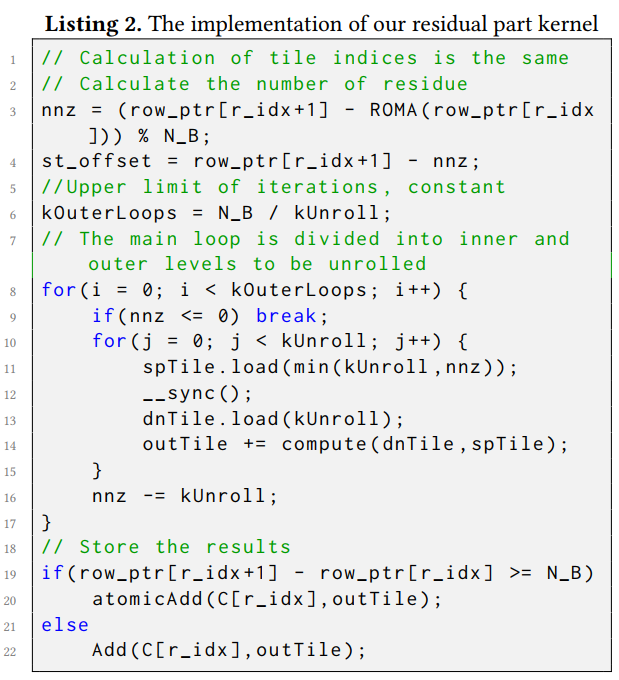
SpMMresidual.png

7-17行利用了Sputnik中的residue unroll技术

18-22行则尽可能减少atomicAdd指令的使用避免性能下降

SDDMM Kernel实现

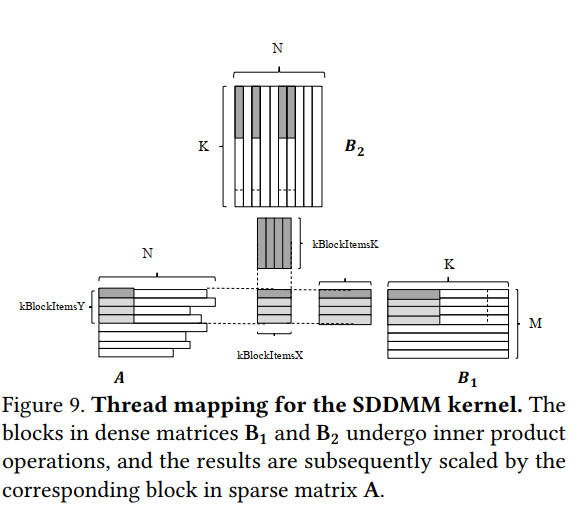
SDDMMblock.png

SDDMM的逻辑大部分都与SpMM相同，不同处：

in B_1 each thread loads  kBlockItemK / #threadsOfSubwarp elements
in B_2 each thread loads kBlockItemX * kBlockItemK / #threadsOfSubwarp elements

两种loads是以交错方式进行的，以合并内存访问，因此最终需要用shuffle指令来交换和归约线程之间的结果，相应的实现如下图所示。

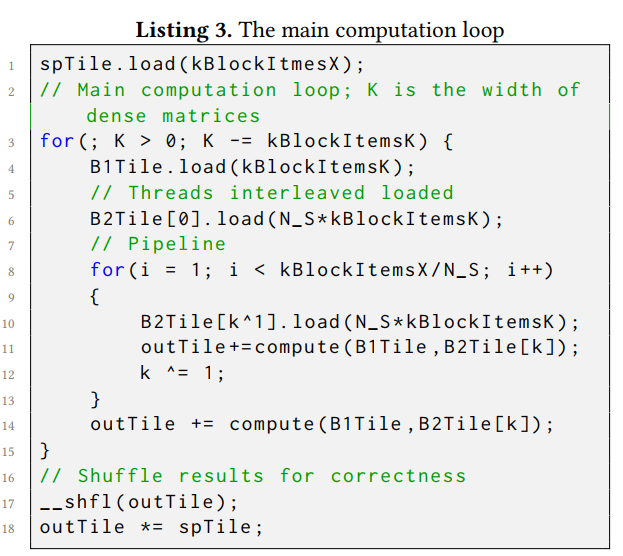
SDDMMkernel.png

总结

本文对于单节点稀疏矩阵乘法的优化是从非零元素的分布来入手的，根据对SuiteSparse中稀疏矩阵的研究，发现了稀疏矩阵的3个特征，总结来说就是短行较多且占主要部分，长行普遍存在但占比较小。先前对于稀疏矩阵乘法的研究没有考虑到这一问题，造成了性能浪费和负载不均衡。因此本文从负载均衡的角度对矩阵进行了分块，分为block part和residual part，分别进行处理，并提出了sub-block pipeline技术来实现访存-计算重叠，从而有效提高SpMM和SDDMM的性能。

CATALOG
    FEATURED TAGS
    Tools Lecture CV DL